Sizi salamlayıram, hörmətli Oxucular!
Bu gün çoxlarının marağına səbəb olan və tez-tez qarşılaşdığımız bir sual barədə danışmaq istəyirəm:
Üçfazalı şəbəkədə iki faza qoşulma zamanı necə 380 voltluq xətti gərginlik alınır?
Axı, riyaziyyata baxsaq, 220 V + 220 V = 440 V etməlidir. Amma burada bir uyğunsuzluq var, elə deyilmi?
Əslində isə hər şey göründüyündən daha sadədir. Doğru hesablamalar 9-cu sinif riyaziyyatı və fizikanın bəzi qanunlarına əsaslanır. Gəlin, başlayaq!
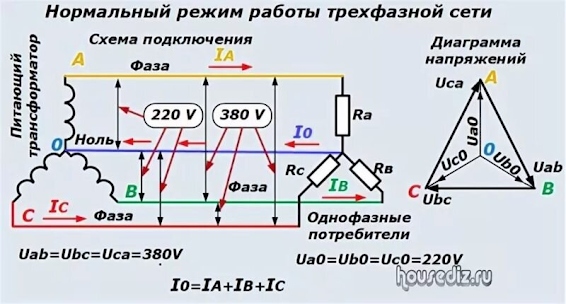
Yuxarıdakı şəkildə iki növ şəbəkəni görürük: birfazalı şəbəkə, burada gərginlik faza gərginliyi (220 volt) ilə neytral arasındakı fərq kimi formalaşır, və üçfazalı şəbəkə, burada eyni anda iki variant - 220 volt və 380 volt - enerji tələb edən yüklər üçün istifadə edilə bilər.
Bunu anlamaq üçün, üçfazalı dəyişən cərəyanın zaman diaqramının necə olduğunu başa düşmək lazımdır:
Şəkildən göründüyü kimi, birinci olaraq "A" sinusoidu sıfır nöqtəsindən keçir, daha sonra isə "B" və "C" sinusoidləri. Bu nöqtələr arasındakı məsafə sabitdir və və ya 120 dərəcəyə bərabərdir.
Niyə məhz 120 dərəcə standartdır?
Səbəb yenə də riyaziyyatla bağlıdır! Əgər , və vektorlarını toplasaq, nəticə sıfır olar. Bu, neytral naqilin istifadəsinə imkan verir və neytralla fazalar arasından 220 voltluq gərginlik əldə etməyə şərait yaradır. Bu, aşağıdakı şəkildə göstərildiyi kimi mümkün olur!
İndi isə 380 voltun necə alındığını araşdıraq. Bunun üçün iki fazanı çəkək və onlara, məsələn, istilik cihazı kimi bir yük qoşaq:
Kirxhofun ikinci qaydası belə deyir:
"Qapalı konturdakı rezistiv elementlərdə (istilik cihazında) gərginliklərin cəmi, həmin kontura daxil olan iki fazanın (bizim fazalarımızın) elektrik hərəkət qüvvələrinin (EHQ) cəbri cəminə bərabərdir."
Bu qaydanın praktiki tətbiqi üçün konturun baxış istiqamətini təsadüfi şəkildə seçdik və fazaların elektrik hərəkət qüvvəsinin (EHQ) müsbət istiqamətini "dolağın başlanğıcı - dolağın sonu" marşrutu olaraq qəbul etdik. Bundan sonra, gərginlik düşgüsünün fazalar arasındakı fərqə bərabər olduğu ifadəni yazdıq.
Ancaq unutmaq olmaz ki, bu, vektor fərqidir! Buna görə də hesablamalar tamamilə başqa cür aparılır.
